5.Cloth Simulation_冲突文件_zkx_20240828215918

布料模拟 二维的面在三维中展开的状态

• A Mass-Spring System

  • Explicit Integration

  • Implicit Integration

• Bending and Locking Issues

• Shape matching

A Mass Spring System

弹簧质点系统

一个理想的弹簧， 胡克定律：试图恢复原状，拉的越长力越大 F = kx 拉越长能量越大

image.png

xi 的能量是各个弹簧的能量累加

Structured Spring Networks

结构化表示弹簧网络

假设衣物是结构化的

image.png

右边是更优化的，能够减少很多弹簧

不规则的弹簧连接

image.png

利用内部边的对角构建抗弯曲的弹簧

通过 Vertex list 和 Triangle list 信息生成弹簧

image.png

不能直接拿三角形边的信息，因为会有重复边

构建 Triple list，删除重复数据，用排序的方式删除 同时生成内部边的垂直弹簧

image.png

显示积分更新所有质点信息

image.png

显示积分的弊端 如果时间步长太大，第二次模拟质点会过远，并超过之前的绝对值

image.png

隐式积分 Implicit Integration

在当前时刻 f [1] 是不知道的

image.png

holonomic 只和位置有关系的力 把 f 写成 f(x_1)，不是线性的力

认为 x[1] 是 F(x) 的最小值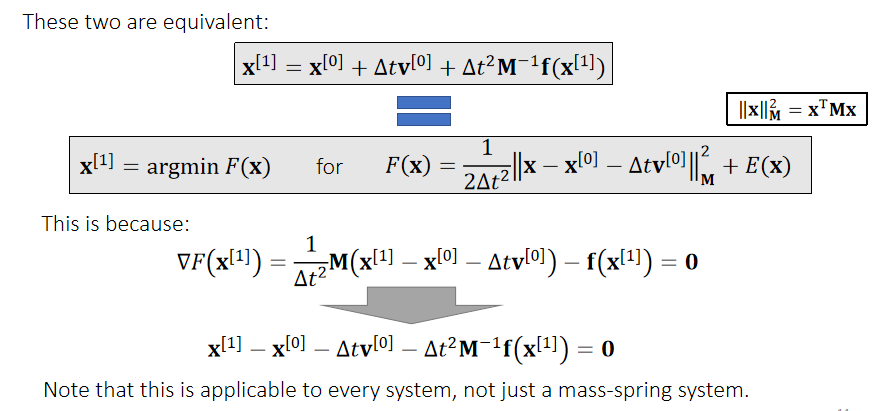

这个隐式积分做法是把数值解转化为解析解，目标是求得 x_1 ，认为在 x_1 处，对于力的函数的求导为 0，也就是弹簧能够平衡的位置，以此来更新速度。

认为下一帧的 x 一定是受力平衡点，以此来求得能够达到目标点的速度。而不是显示积分，通过时间步长，由受力推出速度。

但是由一阶导数式反推出 F(x) 很难，这边是已经知道了

Newton-Raphson Method 牛顿法 数值解逼近目标值，利用一阶的泰勒展开

image.png

一阶导为 0 可能是最大值或最小值，此时看二阶导

image.png

只能找到局部最小值，local minimal ，没有什么好的方法找到全局最小值。 限定二阶导永远大于 0，可以限定只有一个最小值。

三维的牛顿法

用牛顿迭代法来求 x_1

image.png

非线性优化问题，各种解各种物理系统的核心

弹簧系统的 Hessian

image.png

弹簧的 Hessian 矩阵是弹簧 F(x) 的二阶导

在拉伸的时候，它是正定的，表示其有唯一解

image.png

挤压上不正定，可能有各种状态

image.png

用 Jacobi 方法多次迭代

image.png

Jacobi 可以用 GPU 加速