Vector

image.png

左手系统有个好处，当屏幕看作最前方时，所有的物体的坐标都是正值

stack vector ，描述一个几何体，也可以没什么含义

image.png

向量加减法

image.png

向量、点、t 描述粒子的线性运动或者线段或者插值

image.png

向量长度

image.png

生成单位向量

image.png

点积

image.png

求模和判断是否平行

image.png

投影

image.png

判断点 p 与平面 cn 的关系

image.png

粒子运动轨迹和圆的碰撞

image.png

叉积

• 垂直，面积

• 相反

• 分配律

• 平行判定

image.png

计算三角形的法线和面积

image.png

判断点是否在三角形里面

image.png

image.png

重心坐标，重心坐标插值

image.png

Gouraud Shading 重心坐标插值

1. 四面体体积计算 Tetrahedral

image.png

也可以写成 4 * 2 的行列式

负体积的四面体 x3 和底面 normal 同侧为正体积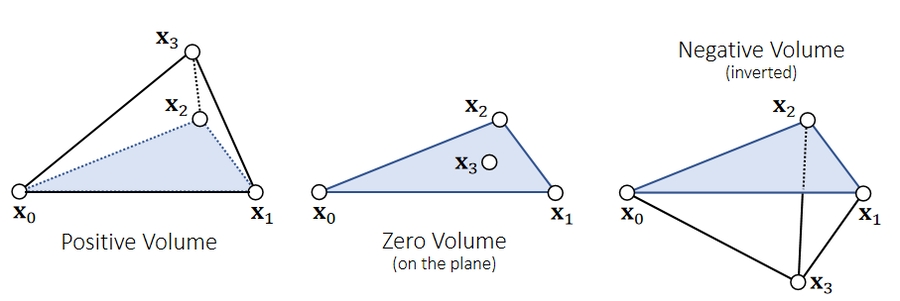

四面体的重心坐标

image.png

粒子 P 点和三角形是否发生碰撞

1. P 和三角形组成的四面体体积为 0 时， P 和三角形所在平面发生碰撞

2. P 点要处在三角形中

Matrix

矩阵

Definition 定义

• Transpose 转置

• Diagonal 对角

• Identity 单位

• Symmetric 对称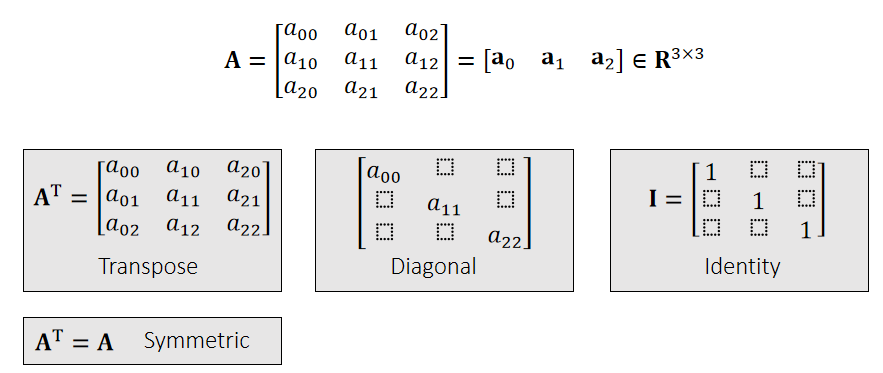

Multiplication 矩阵乘法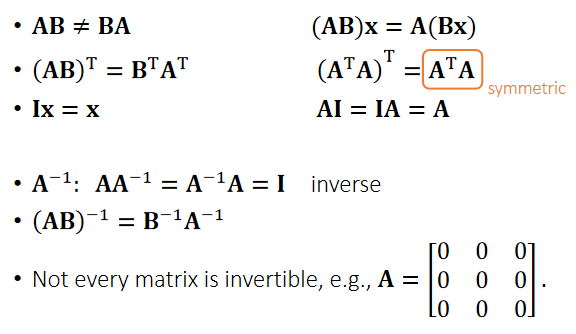

Orthogonality 正交矩阵 由正交向量构成，即都是单位向量，并且它们之间线性无关。 正交矩阵的逆为它转置

Transformation 可以使用正交矩阵来表示旋转

image.png

旋转矩阵就是局部坐标在世界空间中的表示 LocalToWorld Matrix

对角矩阵可以表示三方向的缩放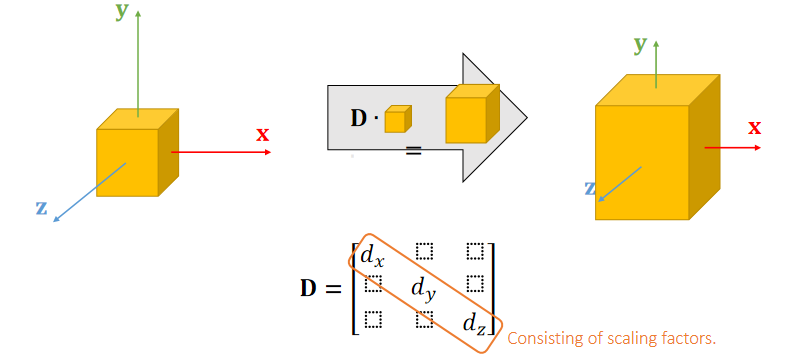

Singular Value Decomposition 奇异值分解

在图形学上的解释，对于任意方向的旋转缩放操作，写成的矩阵。可以分解为 旋转到特定方向的正交矩阵 + 三方向缩放的对角矩阵 + 再次旋转的正交矩阵

image.png

Eigenvalue Decomposition 特征值分解

在图形学上的解释。对于任意的对称矩阵，可以分解为 旋转到特定方向的正交矩阵 + 特定方向缩放的对角矩阵 + 反向旋转回原方向的正交矩阵。其中对角矩阵里的值就是特征值

image.png

Symmetric Positive Definiteness 对称且正定 s.p.d 矩阵被任意向量两边乘后的标量大于 0

image.png

正定矩阵的特征值都大于 0

更广的判定方法是对角占优的矩阵也是正定矩阵 正定矩阵都是可逆的

image.png

如果 A 是对称且正定的，那么 B 是对称且半正定的

image.png

Linear Solver

线性问题 求解 x ，其中 A 是矩阵，b 是边界条件

image.png

最直观的解法是求 A 的逆矩阵，还有直接法和迭代法

Direct Linear Solver 直接法，LU 分解

image.png

如果 A 是稀疏的，LU 不一定稀疏

image.png

Iterative LInear Solver 迭代法逼近

系数 * 迭代矩阵 * 残差

image.png

迭代法 M 需要容易求解，可逆

image.png

1. 简单

2. 不要求精确解

3. 容易并行

4. 需要有收敛性

5. 速度慢

Tensor Calculus

一阶导 1st-Order Derivatives

对向量的求导，求偏导

image.png

梯度 ：gradient 方向，等高线的最快上升方向，上升速度

一阶导拓展

image.png

• 雅可比矩阵 ： Jacobian

• 散度：Divergence，雅可比矩阵对角和

• 旋度：Curl

二阶导

image.png

Hessian 的对角是拉普拉斯，注意符号

Taylor Expansion 泰勒展开 对 x0 进行泰勒展开，即 x0 处的值 + 不断地使用梯度逼进

image.png

对称且正定在这的二阶项说明二阶项一定是正的

向量模长对向量的求导，即向量长度的梯度，即沿着向量方向的单位向量

image.png

弹簧

image.png

H 矩阵是 Tangent stiffness 胡可系数 弹簧对 x 的方程是能量 对 x 的一阶导结果是力， 对 x 的二阶导是胡可系数，力函数的切向量。

两个点的弹簧

image.png